动态规划(Dynamic Programming)是一种分阶段求解决策问题的数学思想,它通过把原问题分解成简单的子问题来简化求解的难度。如果某一问题有很多重叠子问题,使用动态规划是最有效的。所以动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心,贪心没有状态推导,而是从局部直接选最优的。
动态规划问题,可以拆解为五步:
- 确定dp数组以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
接雨水
题目描述:给定
n个非负整数表示每个宽度为1的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
1
2
3输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。思路:
按列来计算每一列能接的雨水,最后全部列相加即可得到结果。而每一列的雨水,根据木桶短板效应,可知由左右两边最高柱子中相对较低的那一根与所在列柱子高度决定。于是我们需要知道不同列的左右两边最高的柱子高度是多少,这里可以建立两个动态规划方程:某一列左边最高的柱子与右边最高的柱子。设定左边最高柱子与所在列的关系为动态规划数组:maxLeft,maxLeft[i]即代表在第i列的时候,左边最高的柱子高度为maxLeft[i]。则可以得出推导公式:maxLeft[i] = max(maxLeft[i-1], nums[i]),推导顺序从左到右。同理,某一列右边最高的柱子动态规划数组为:maxRight。推导公式为:maxRight[i] = max(maxRight[i+1], i+1),推导顺序从右到左。最后,某一列所能接的雨水数量results[i] = (min(maxLeft[i], maxRigth[i]) - nums[i]) (当min(maxLeft[i], maxRigth[i]) > nums[i]时,如果小于等于,则results[i]=0)
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39class Solution {
public int trap(int[] height) {
// 计算每一列的水量,每一列的水量由左右两边最高的一堵墙以及所在列的墙高决定。
// maxLeft[] 数组用来存储下标为i的列的左边最高墙的高度
// maxRight[] 数组用来存储下标为i的列的右边最高墙的高度
if (height.length<3){
return 0;
}
int sum=0;
int maxLeft[] = new int[height.length];
int maxRight[] = new int[height.length];
maxLeft[1] = height[0];
maxRight[height.length-2] = height[height.length-1];
for (int i=2; i < height.length; i ++){
maxLeft[i] = Math.max(maxLeft[i-1], height[i-1]);
}
for (int j=height.length-3; j>=0; j--){
maxRight[j] = Math.max(maxRight[j+1], height[j+1]);
}
for(int i=1; i < height.length-1; i++){
int min = Math.min(maxLeft[i], maxRight[i]);
if (min < height[i]){
sum += 0;
}else{
sum += (min - height[i]);
}
}
return sum;
}
}最大子数组和
题目描述:给你一个整数数组
nums,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。子数组 是数组中的一个连续部分。
1
2
3输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。思路:题目只要求返回结果,不要求得到最大的连续子数组是哪一个。这样的问题通常可以使用「动态规划」解决。根据动态规划的思想,可以计算出在每一个数组下标处,最大和的连续子数组和为dp[i]。由于题目要求是连续的子数组,因此,对于每一个下标i,当前的最大和要么为dp[i-1] + nums[i],要么则是 dp[i]。
假设
nums数组的长度是n,下标从0到n-1。我们用
f(i)代表以第i个数结尾的「连续子数组的最大和」,那么很显然我们要求的答案就是: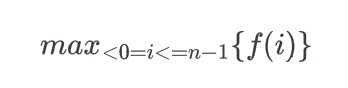
因此,我们只需要求出每个位置的f(i),然后返回f数组中的最大值即可。我们如何求f(i)呢?我们可以考虑nums[i]单独成为一段或者是加入f(i-1)对应的那一段,这取决于nums[i]和f(i-1) + nums[i]的大小关系,我们希望获得一个比较大的,于是可以写出这样的动态规划转移方程: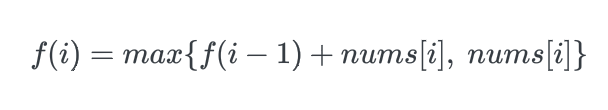
代码如下:1
2
3
4
5
6
7
8
9
10
11
12class Solution {
public int maxSubArray(int[] nums) {
int pre=0;
int maxAns = nums[0];
for (int x:nums){
pre = Math.max(pre+x, x);
maxAns = Math.max(maxAns, pre);
}
return maxAns;
}
}编辑距离
题目描述:
给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数。
你可以对一个单词进行如下三种操作:
插入一个字符
删除一个字符
替换一个字符思路:
动态规划经典的题目,
dp[i][j]数组用来表示word1到下标i-1处的字符串转换成word2到下标j-1处的字符串所需要的最少操作数。为了计算方便,dp[0][0]表示的是空字符串到空字符串的转换所需要的最少操作数。可以画出如下图:
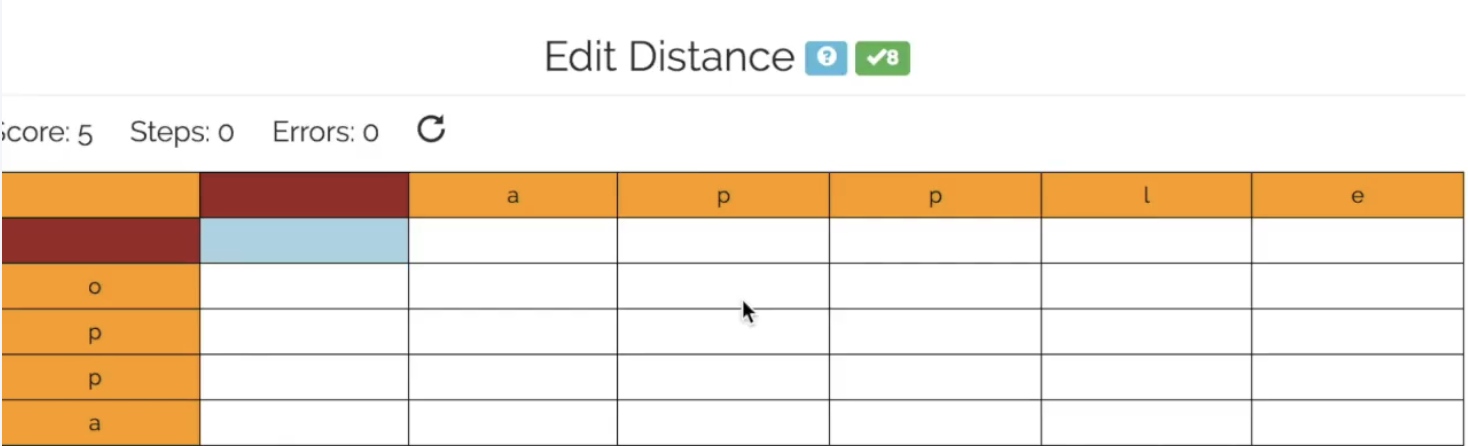
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36class Solution {
public int minDistance(String word1, String word2) {
int[][] dp = new int[word1.length()+1][word2.length()+1];
for (int i=1; i<=word2.length(); i++){
// 空字符串到word2[i]需要的操作次数
dp[0][i] = i;
}
for(int i=0; i<=word1.length(); i++){
// word1[i]到空字符串需要的操作次数
dp[i][0] = i;
}
// 开始计算dp[i][j]所需要的操作次数
for(int i=1; i <= word1.length(); i++){
for (int j=1; j <= word2.length(); j++){
// 分两种情况探讨
// 1. word1[i] == word2[j]
if (word1.charAt(i-1) == word2.charAt(j-1)){
dp[i][j] = dp[i-1][j-1];
} else {
dp[i][j] = minProcess(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1;
}
}
}
return dp[word1.length()][word2.length()];
}
public int minProcess(int a, int b, int c) {
int min = a > b ? b : a;
min = min > c ? c : min;
return min;
}
}