二叉树类算法

1.1 基本知识

二叉树（Binary Tree）是n（n≥0）个有限元素的集合，该集合或者为空，或者由一个称为根（root）的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成。当集合为空时，称该二叉树为空二叉树。

1.2 常见概念

• 结点的度。结点所拥有的子树的个数称为该结点的度。
• 叶子结点。度为0的结点称为叶子结点，或者称为终端结点。
• 分支结点。度不为0的结点称为分支结点，或者称为非终端结点。一棵树的结点除叶子结点外，其余的都是分支结点。
• 左孩子、右孩子、双亲。树中一个结点的子树的根结点称为这个结点的孩子。这个结点称为它孩子结点的双亲。具有同一个双亲的孩子结点互称为兄弟。
• 路径、路径长度。如果一棵树的一串结点n1,n2,…,nk有如下关系：结点ni是ni+1的父结点（1≤i＜k），就把n1,n2,…,nk 称为一条由n1 至nk 的路径。这条路径的长度是k-1。
• 祖先、子孙。在树中，如果有一条路径从结点M到结点N，那么M就称为N的祖先，而N称为M的子孙。
  结点的层数。规定树的根结点的层数为1，其余结点的层数等于它的双亲结点的层数加1。
• 满二叉树。在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有叶子结点都在同一层上，这样的一棵二叉树称作满二叉树。
• 完全二叉树。叶子结点只能出现在最下层和次下层，且最下层的叶子结点集中在树的左部。需要注意的是，满二叉树肯定是完全二叉树，而完全二叉树不一定是满二叉树。
• 二叉搜索树。又：二叉查找树，二叉排序树它或者是一棵空树，或者是具有下列性质的二叉树： 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树。二叉搜索树作为一种经典的数据结构，它既有链表的快速插入与删除操作的特点，又有数组快速查找的优势；所以应用十分广泛，例如在文件系统和数据库系统一般会采用这种数据结构进行高效率的排序与检索操作。

1.3 遍历方法

二叉树的遍历可以分为四种方法：

1. 层序遍历（需要使用队列）
2. 先序遍历
3. 中序遍历
4. 后序遍历

后面三种遍历方式的代码模版如下：

// 先序遍历
public void preOrder(TreeNode root, List<Integer> result){
      if (root == null){
            return;
      }
      result.add(root.val);
      inorder(root.left, result);
      inorder(root.right, result);
}

// 中序遍历
public void inOrder(TreeNode root, List<Integer> result){
      if (root == null){
            return;
      }

      inorder(root.left, result);
      result.add(root.val);
      inorder(root.right, result);
}

// 后序遍历
public void aftOrder(TreeNode root, List<Integer> result){
      if (root == null){
            return;
      }

      inorder(root.left, result);
      inorder(root.right, result);
      result.add(root.val);
}

可以发现三种遍历方式只是在对当前数据与左右子树数据的处理顺序上有所差异

1.4 相关题目

1. 验证二叉搜索树

   给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

   有效 二叉搜索树定义如下：

   • 节点的左子树只包含 小于 当前节点的数。
   • 节点的右子树只包含 大于 当前节点的数。
   • 所有左子树和右子树自身必须也是二叉搜索树。

   解题思路：

   根据二叉搜索树的特性，可知我们需要遍历每一个节点，判断其是否满足条件，根据二叉搜索树的定义，可以知道对于每一个节点，它都需要满足在一个取值范围内，设为[lower, upper]，注意这里为开区间。对于某个节点的左子树，取值范围应该更改为[lower, node.val]，而其右子树的取值范围应该更改为[node.val, upper]。

   一开始的取值范围应该为负无穷到正无穷，所以我们需要学习java中正、负无穷的代码：

   Long.MIN_VALUE  // 负无穷
   Long.MAX_VALUE	 // 正无穷

   代码如下：

   class Solution {
       public boolean isValidBST(TreeNode root) {
           return !isInValid(root, Long.MIN_VALUE, Long.MAX_VALUE);
       }
   
       public boolean isInValid(TreeNode root, long lower, long upper){
           if (root == null){
               return false;
           }
   
           if (root.val <= lower || root.val >= upper){
               return true;
           }
           
           return isInValid(root.left, lower, root.val) || isInValid(root.right, root.val, upper);
       }
   }

2. 二叉树的层序遍历

   题目描述；

   给你二叉树的根节点 root ，返回其节点值的 层序遍历。（即逐层地，从左到右访问所有节点）。

   示例：

   

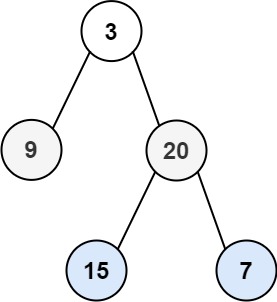
   输入：root = [3,9,20,null,null,15,7]
   输出：[[3],[9,20],[15,7]]

   思路：二叉树的层序遍历需要使用到队列FIFO的特性。这里顺便总结一下队列以及栈在java中的实现代码。这两者实际都是使用链表作为底层实现。

   // 栈使用Deque（Queue下面的一类，双端队列）
   Deque<TreeNode> stack = new LinkedList<>();
   stack.push(TreeNode node); // 将元素压入栈
   stack.pop(); // 移除栈顶元素并返回其值
   stack.peek(); // 获得栈顶元素值
   
   
   // 队列使用Queue
   Queue<TreeNode> queue = new LinkedList<>();
   queue.offer(TreeNode node); // 在队列尾端插入元素
   queue.poll(); // 移除队首元素并返回其值
   queue.peek(); // 获得队首元素值

   步骤：

   • 首先根元素入队
   • 当队列不为空的时候
     • 求当前队列的长度 $s_{i}$
     • 依次从队列中取 $s_{i}$ 个元素进行拓展，然后进入下一次迭代

   代码如下：

   class Solution {
       public List<List<Integer>> levelOrder(TreeNode root) {
           List<List<Integer>> result = new ArrayList<>();
           if (root == null){
               return result;
           }
   
           Queue<TreeNode> queue = new LinkedList<>();
           queue.offer(root);
           while (!queue.isEmpty()){
               List<Integer> list = new ArrayList<>();
               int currentSize = queue.size();
               for (int i=0; i < currentSize; i++){
                   TreeNode current = queue.poll();
                   list.add(current.val);
                   if (current.left!=null){
                       queue.offer(current.left);
                   }
   
                   if (current.right!=null){
                       queue.offer(current.right);
                   }
               }
               
               result.add(list);
           }
   
           return result;
       }
   }

3. 从前序与中序遍历序列构造二叉树

   题目描述：给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

   提示：

   • 1 <= preorder.length <= 3000
   • inorder.length == preorder.length
   • -3000 <= preorder[i], inorder[i] <= 3000
   • preorder 和 inorder 均 无重复 元素
   • inorder 均出现在 preorder
   • preorder 保证 为二叉树的前序遍历序列
   • inorder 保证 为二叉树的中序遍历序列

   示例：

   输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
   输出: [3,9,20,null,null,15,7]

   解题思路：

   根据先序遍历以及中序遍历的特点可以知道，先序遍历的第一个节点就是根结点，而根据这个根结点可以在中序遍历找到其位置，以根结点为区分，中序遍历左边的树为其左子树，中序遍历右边的树为其右子树。递归的构造二叉树。

   因为提示说到二叉树中无重复元素，可以使用哈希表存储每个值及其对应的在中序遍历数组中的位置，这样可以很快找到根结点的位置。

   代码如下：

   class Solution {
       Map<Integer, Integer> map_in = new HashMap<>();
       public TreeNode buildTree(int[] preorder, int[] inorder) {
           for (int i=0; i < inorder.length; i++){
               map_in.put(inorder[i], i);
           }
   
           return build(preorder, inorder, 0, preorder.length-1, 0, inorder.length-1);
       }
   
        public TreeNode build(int[] pre, int[] in, int startP, int endP, int startI, int endI){
           if (startP > endP || startI > endI){
               return null;
           }
           // 先序遍历数组第一个值就是根结点
           int rootNum = pre[startP];
           // 根据哈希表找到根结点在中序遍历数组中的位置
           int root_in = map_in.get(rootNum);
   
           // 创建根结点
           TreeNode root = new TreeNode(rootNum);
   
           // 根结点左边为左子树
           int left_size = root_in - startI;
           root.left = build(pre, in, startP+1, startP+left_size, startI, root_in-1);
   
           // 根结点右边为右子树
           int right_size = endI - root_in;
           root.right = build(pre, in, startP+left_size+1, endP, root_in+1, endI);
   
           return root;
       }
   }