单调队列 | VyacheslavK's Notes

经典题目

滑动窗口最大值

题目描述：

给定一个数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回滑动窗口中的最大值。

示例：

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

解题思路：

这个是使用单调队列的经典题目。用暴力方法来求解的话，遍历一遍的过程每次从窗口中找到最大的数值，很明显时间复杂为O(n*k)。此时，我们可以考虑使用一个单调队列，这个队列，放进去窗口里的元素，随着窗口的移动，队列里的元素一进一出，每次移动之后，队列可以返回里面的最大值。

队列的基本框架应该是：

public class MyQueue {
    void pop(int value) {
    }
    void push(int value) {
    }
    int front() {
        return que.front();
    }
};

每次窗口移动的时候，调用que.pop(滑动窗口中移除元素的数值)，que.push(滑动窗口添加元素的数值)，然后que.front()就返回我们要的最大值。遗憾的是，没有现成的这种队列结构供我们使用，需要我们自己实现。

那我们就要开始考虑到，如何随着窗口的滑动，能够得到窗口中的最大值了。

其实，我们只需要维护窗口中可能成为最大元素的值就行了，随着窗口向右滑动，左边的元素会被一个一个的清除掉，因此，我们可以建立一个单调递减的队列，队首元素即是窗口中的最大值，每次滑动窗口，都是在向队尾添加元素，如果队列中有比当前添加元素更小的元素就应该弹出直到队列为空或者队列中没有比其更小的元素，再将添加元素放进队尾。这样保证了滑动窗口存储了当前可能的最大值，先前进入队列的元素肯定是在当前添加元素的左边，这样保证了如果当前添加元素比左边的元素大，那么只要当前元素存在则较大值一定是当前元素，随着窗口右滑，当前元素左边的元素会一个一个不再出现在窗口中，我们也不需要维护这些元素。

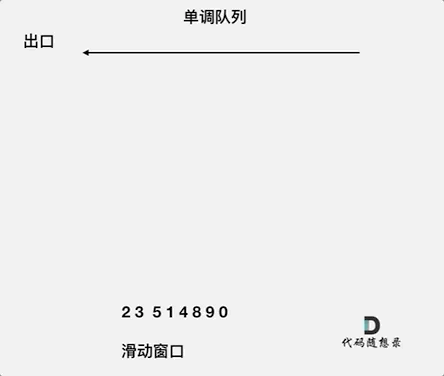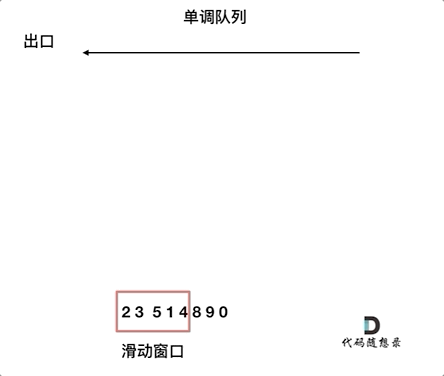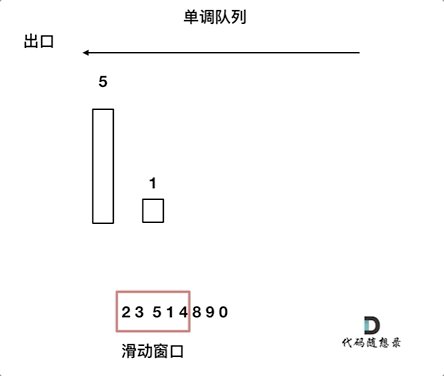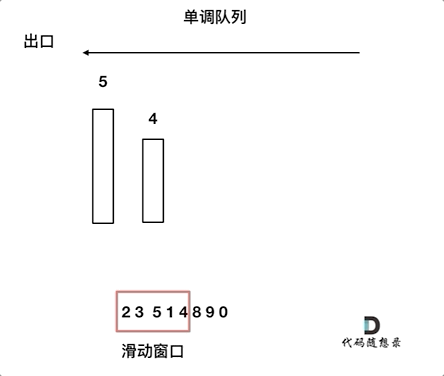
239.滑动窗口最大值

对于窗口里的元素{2, 3, 5, 1 ,4}，单调队列里只维护{5, 4} 就够了，保持单调队列里单调递减，此时队列出口元素就是窗口里最大元素。

此时大家应该怀疑单调队列里维护着{5, 4} 怎么配合窗口经行滑动呢？

设计单调队列的时候，pop，和push操作要保持如下规则：

pop(value)：如果窗口移除的元素value等于单调队列的出口元素，那么队列弹出元素，否则不用任何操作
push(value)：如果push的元素value大于入口元素的数值，那么就将队列入口的元素弹出，直到push元素的数值小于等于队列入口元素的数值为止

保持如上规则，每次窗口移动的时候，只要问que.front()就可以返回当前窗口的最大值。

为了更直观的感受到单调队列的工作过程，以题目示例为例，输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3，动画如下：

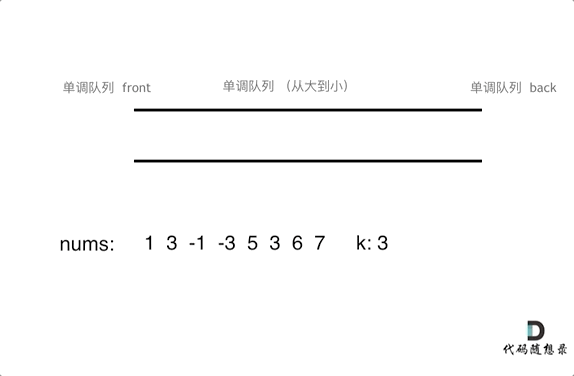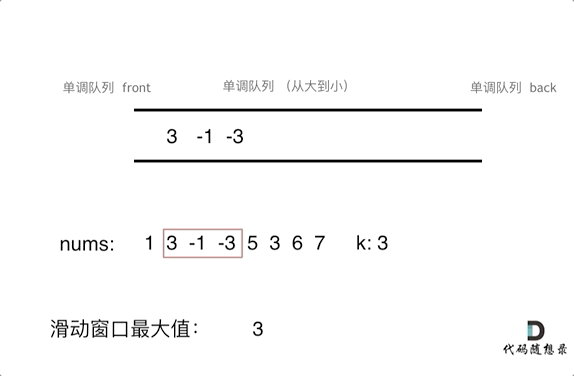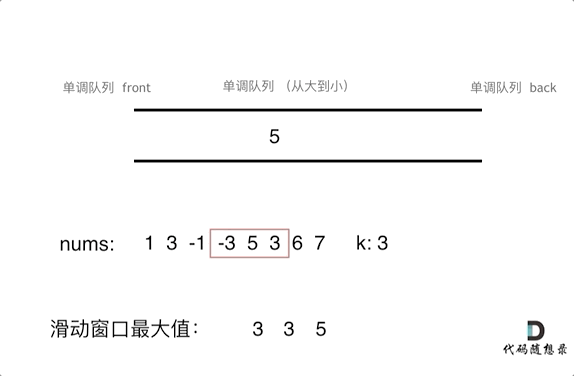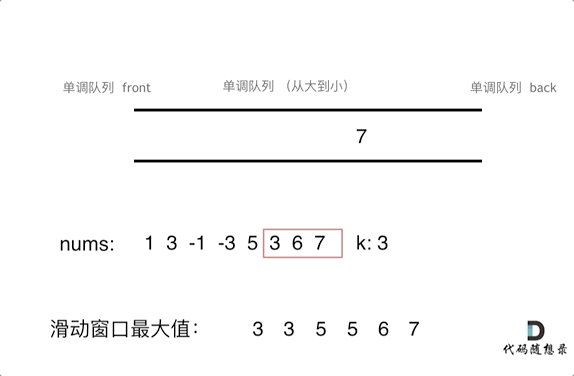
239.滑动窗口最大值-2

实现这一数据结构我们需要使用到Deque：

class MyQueue {
    Deque<Integer> deque = new LinkedList<>();
    //弹出元素时，比较当前要弹出的数值是否等于队列出口的数值，如果相等则弹出
    //同时判断队列当前是否为空
    void poll(int val) {
        if (!deque.isEmpty() && val == deque.peek()) {
            deque.poll();
        }
    }
    //添加元素时，如果要添加的元素大于入口处的元素，就将入口元素弹出
    //保证队列元素单调递减
    //比如此时队列元素3,1，2将要入队，比1大，所以1弹出，此时队列：3,2
    void add(int val) {
        while (!deque.isEmpty() && val > deque.getLast()) {
            deque.removeLast();
        }
        deque.add(val);
    }
    //队列队顶元素始终为最大值
    int peek() {
        return deque.peek();
    }
}

最后代码实现如下：

class Solution {
    // 自己实现一种单调队列
    class MyQueue{
        Deque<Integer> deque = new LinkedList<>();

        // 往队列尾部添加元素
        public void push(int num){
            // 要保持队列单调的性质
            while(!deque.isEmpty() && deque.getLast() < num){
                deque.removeLast();
            }
            deque.add(num);
        }

        // 滑动窗口右移时，判断移除的元素是否等于当前队首元素
        public void pop(int num){
            // 如果相等，移除队首元素
            if (!deque.isEmpty() && num==deque.peek()){
                deque.poll();
            }
            // 不相等，则不做任何操作
        }

        // 获取当前队列的最大值
        public int peek(){
            return deque.peek();
        }
    }

    public int[] maxSlidingWindow(int[] nums, int k) {
        int max = nums[0];
        if(nums.length <= k){
            for (int i=0; i < nums.length; i++){
                if (nums[i] > max){
                max = nums[i];
                }
            }
        
            return new int[]{max};
        }

        int len = nums.length - k + 1;
        int[] result = new int[len];
        MyQueue queue = new MyQueue();
        for (int i=0; i < k; i++){
            queue.push(nums[i]);
        }

        result[0] = queue.peek();
        for(int i=1; i < len; i++){
            queue.push(nums[k+i-1]);
            queue.pop(nums[i-1]);
            result[i] = queue.peek();
        }


        return result;

    }
}