单调栈是一种栈式的数据结构,它的特点在于:栈内元素从栈底到栈顶呈现非递增或者非递减。
对于一个一维数组:arr = [2, 1, 5, 6, 2, 3],如何建立一个从栈底到栈顶的非递减栈呢?
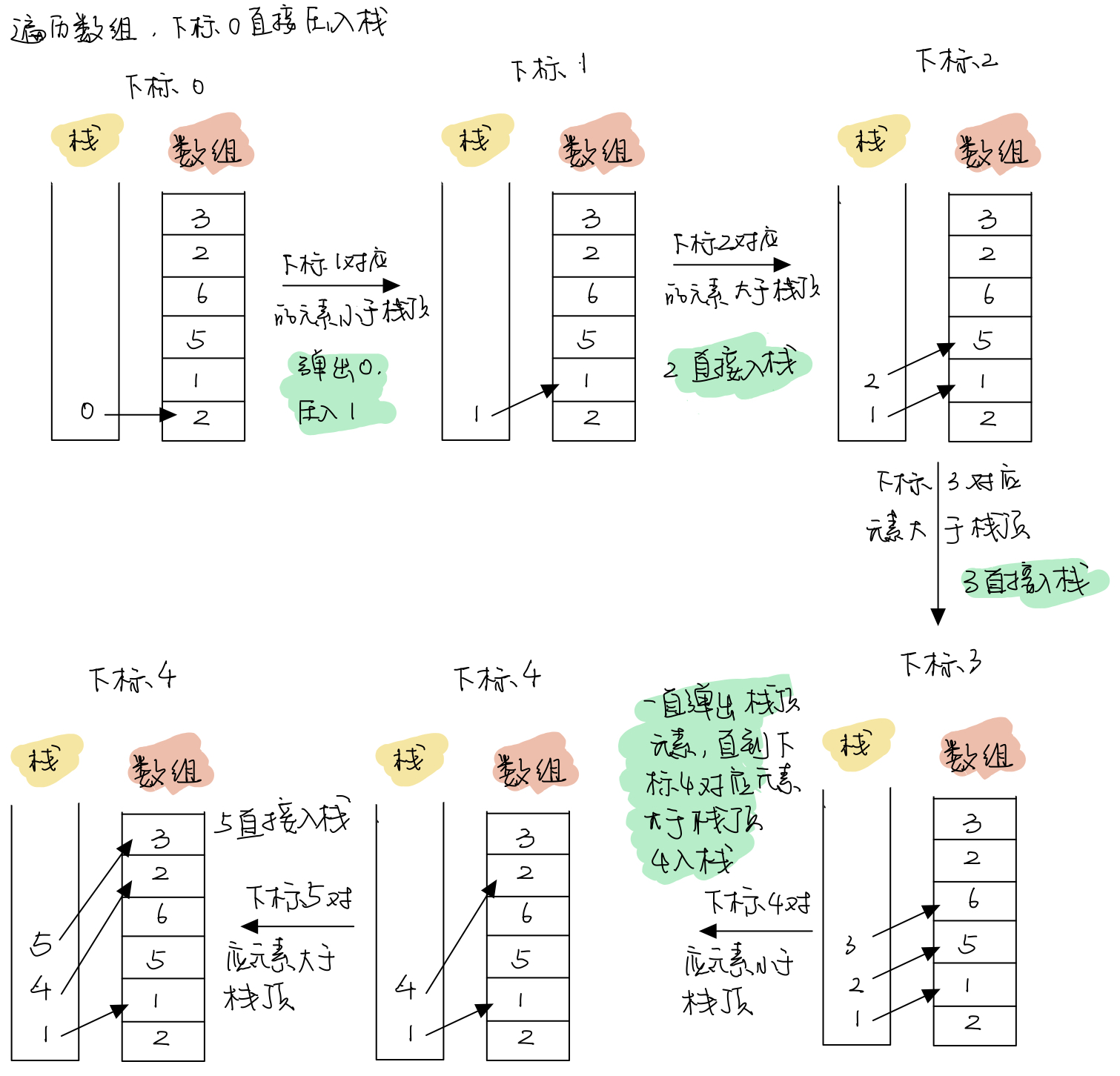
首先,从数组的0下标开始,因为此时栈为空,直接将下标0压入栈中。
接着,数组的1下标,对应的数字为1,对于栈顶元素0下标对应的数字2来说要小,所以弹出0,此时栈为空,直接压入下标1。
数组的2下标:对应的数字为5,对于栈顶元素1下标对应的数字1来说要大,直接压入下标2。
数组的3下标:对应的数字为6,对于栈顶元素2下标对应的数字5来说要大,直接压入下标3。
数组的4下标:对应的数字为2,对于栈顶元素3下标对应的数字6来说要小,所以弹出3,此时栈不为空,且新的栈顶元素2下标对应的数字5还是比2大,所以继续弹出2,直到栈顶元素1下标对应的数字1比2小,此时压入下标4。
数组的5下标:对应的数字为3,对于栈顶元素4下标对应的数字2来说要大,直接压入下标5。
此时,数组的元素从左到右都被遍历了一遍,而且可以注意到对于非递减栈在需要弹出元素的时候,栈顶下标对应的数组元素要小于当前遍历下标对应的数组元素,这时候对于栈顶下标对应的元素就找到了数组中右边第一个小于它的元素,而弹出一次后的栈顶元素则是数组中左边第一个小于它的元素,这三个元素形成了一个凸状大小结构。
单调栈常常运用在这种情景中:通常是一维数组,要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置,此时我们就要想到可以用单调栈了。
我们一般在栈中存储数组的下标,这样既可以记录元素在数组中的位置,又可以通过这个位置找到它对应的数组元素。
1. 相关题目
1.1 柱状图中的最大矩形
题目描述:
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
1
2
3
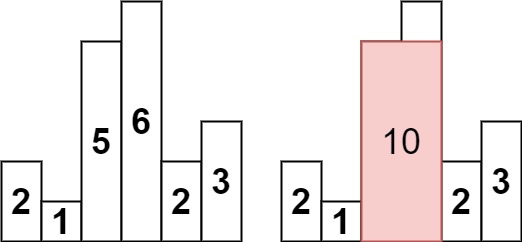
| 输入:heights = [2,1,5,6,2,3]
输出:10
解释:最大的矩形为图中红色区域,面积为 10
|
思路:
对于每一个i来说,它的对应高度是height[i],我们可以找它左右两边第一个比它小的柱子,这样就能得到该位置对应的高度能得到的最大的矩形面积。
如图所示:
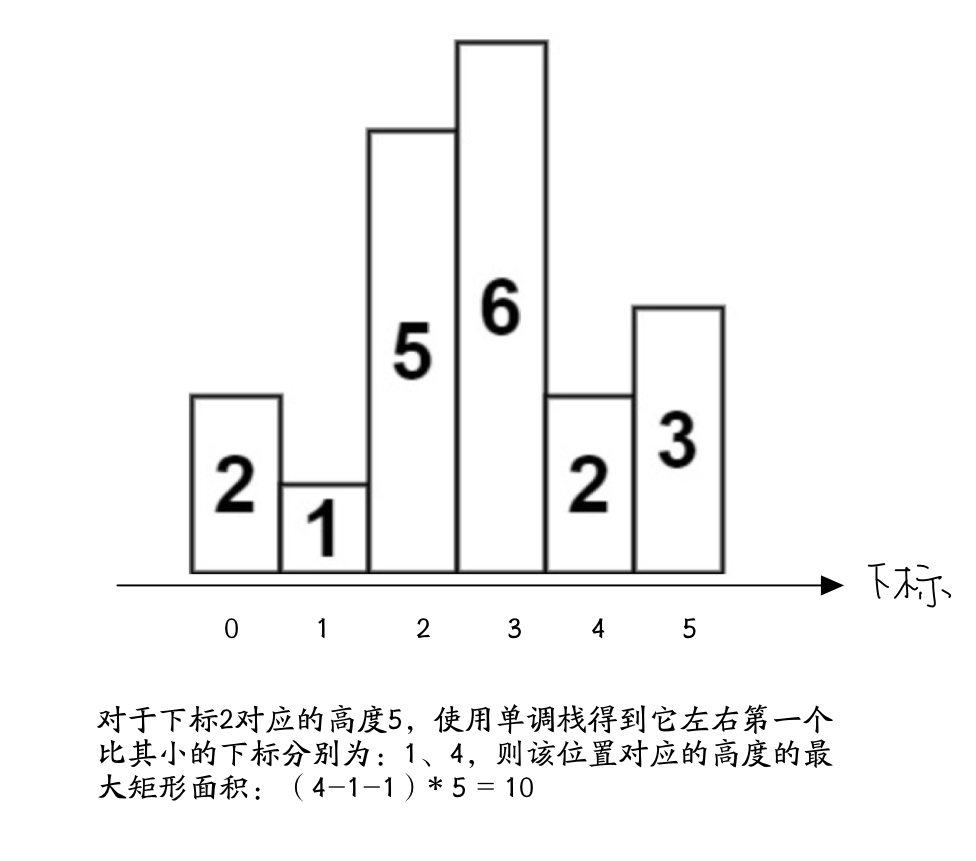
使用非递减栈,从左到右遍历,可以得到每个位置左边第一个比其小的柱子下标,用leftMin数组来存储数据,对于0下标,因为它左边没有柱子了,所以leftMin[0] = -1。 再使用非递减栈,从右到左遍历,可以得到每一个位置右边第一个比其小的柱子下标。同理,可用rightMin数组存储每个位置右边第一个比其小的柱子下标,rightMin[height.length-1] = height.length。
遍历每个位置,(rightMin[i]-leftMin[i]-1) * heigth[i]即为i位置对应高度所能形成的最大矩形面积,取最大值即为想要的结果。
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
| class Solution {
public int largestRectangleArea(int[] heights) {
int[] minLeft = new int[heights.length];
int[] minRight = new int[heights.length];
minLeft[0] = -1;
minRight[heights.length-1] = heights.length;
Deque<Integer> stack = new LinkedList<>();
stack.push(0);
for (int i=1; i < heights.length; i++){
while(!stack.isEmpty() && heights[stack.peek()] >= heights[i]){
stack.pop();
}
if (stack.isEmpty()){
minLeft[i] = -1;
} else {
minLeft[i] = stack.peek();
}
stack.push(i);
}
stack.clear();
stack.push(heights.length-1);
for (int j=heights.length-2; j >= 0; j--){
while (!stack.isEmpty() && heights[j] <= heights[stack.peek()]){
stack.pop();
}
if (stack.isEmpty()){
minRight[j] = heights.length;
} else {
minRight[j] = stack.peek();
}
stack.push(j);
}
int[] results = new int[heights.length];
int max = 0;
for (int i=0; i < heights.length; i++){
results[i] = (minRight[i] - minLeft[i] - 1) * heights[i];
if (results[i] > max){
max = results[i];
}
}
return max;
}
}
|
1.2 最大矩形
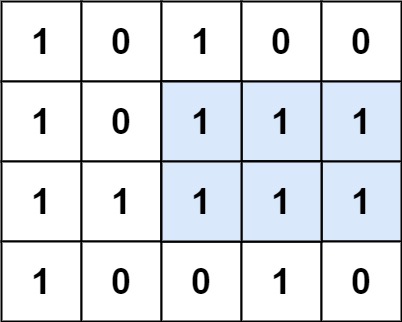
题目描述:给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
示例:
1
2
| 输入:matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出:6
|
解题思路:
这道题其实跟柱状图中的最大矩形是一样的,只是变成了二维的,我们可以考虑从左到右看过去,计算每一行在第j列的位置处连续的1有多少个,从而转换成了一张柱状图:
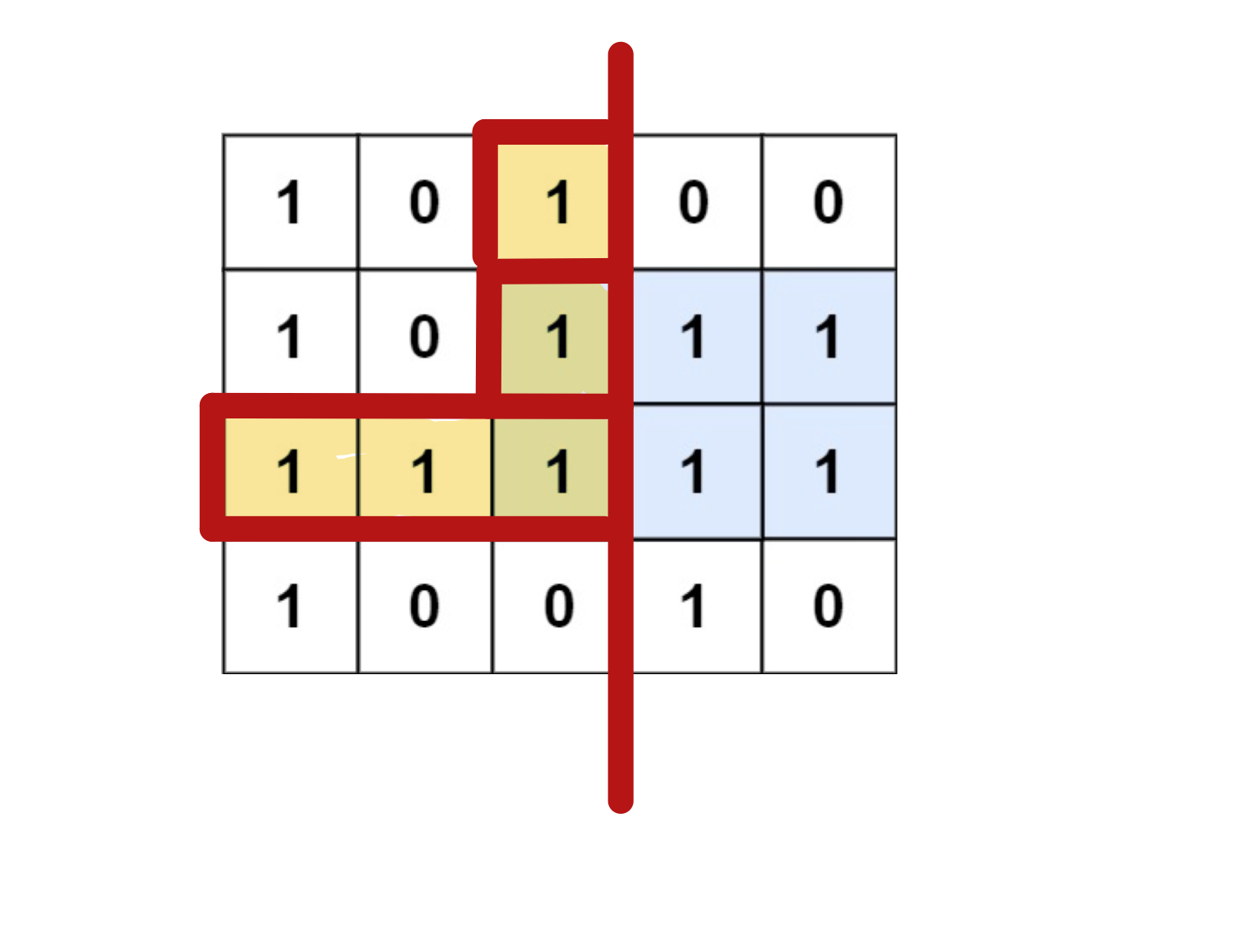
从而计算该柱状图所对应的最大矩形面积,遍历每一列,则能得到每个(i,j)对应高度的最大矩形面积,这里使用的是与柱状图所对应的最大矩形面积一样使用过的单调栈来计算,从而获得整张二维矩阵对应的最大矩形面积。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
| class Solution {
public int maximalRectangle(char[][] matrix) {
int[][] rect = new int[matrix.length][matrix[0].length];
for(int i=0; i<matrix.length; i++){
for(int j=0; j < matrix[0].length; j++){
if (j==0){
rect[i][j] = matrix[i][j]=='1'?1:0;
} else {
if (matrix[i][j]=='1'){
rect[i][j] = rect[i][j-1] + 1;
} else {
rect[i][j] = 0;
}
}
}
}
int[][] upper = new int[matrix.length][matrix[0].length];
int[][] lower = new int[matrix.length][matrix[0].length];
int[][] maxSquare = new int[matrix.length][matrix[0].length];
Deque<Integer> stack = new LinkedList<>();
for (int j=0; j<matrix[0].length; j++){
upper[0][j] = -1;
stack.clear();
stack.push(0);
for(int i=1; i<matrix.length; i++){
while(!stack.isEmpty() && rect[stack.peek()][j] >= rect[i][j]){
stack.pop();
}
if (stack.isEmpty()){
upper[i][j] = -1;
} else {
upper[i][j] = stack.peek();
}
stack.push(i);
}
lower[matrix.length-1][j] = matrix.length;
stack.clear();
stack.push(matrix.length-1);
for (int i=matrix.length-2; i>=0; i--){
while(!stack.isEmpty() && rect[stack.peek()][j] >= rect[i][j]){
stack.pop();
}
if (stack.isEmpty()){
lower[i][j] = matrix.length;
} else {
lower[i][j] = stack.peek();
}
stack.push(i);
}
for (int i=0; i < matrix.length; i++){
maxSquare[i][j] = (lower[i][j] - upper[i][j] - 1) * rect[i][j];
}
}
int max = 0;
for (int i=0; i < matrix.length; i++){
for (int j=0; j < matrix[0].length; j++){
if (max < maxSquare[i][j]){
max = maxSquare[i][j];
}
}
}
return max;
}
}
|




