案例描述:
邓老师是夜曲中学初一年级的年级主任,上个月期末考试后,他收集了4个班:文科(语文+英语),理科(数学+物理)的考试成绩。
他打算通过分析月考的情况,制定下个月的教学策略。
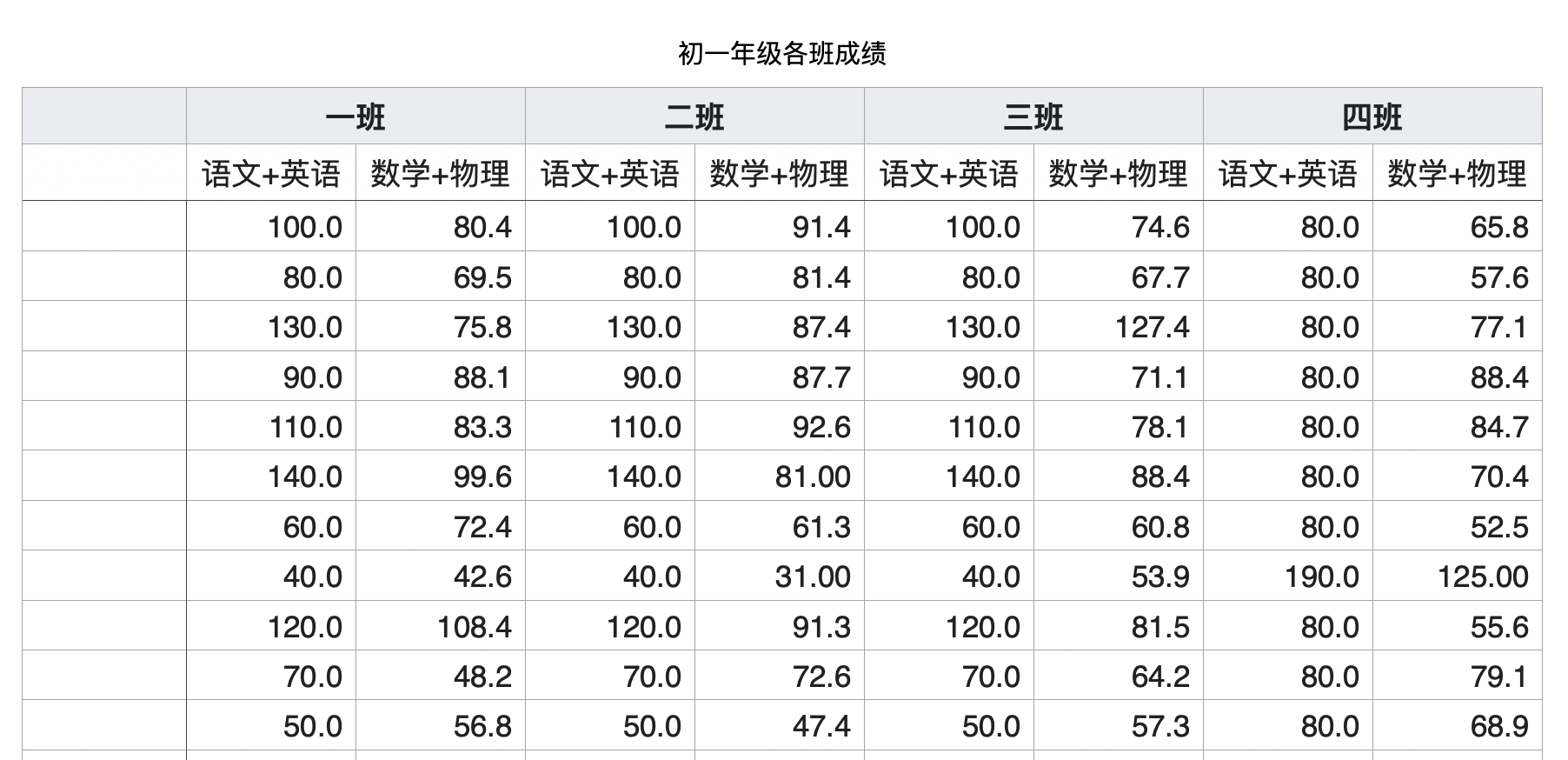
总分和平均分
根据以往的经验,他先计算各个班的总分和平均分,了解各班成绩的总体情况。
非常巧合的是:每个班语文+英语的总分都是990,平均分为90.00。
数学+物理的总分约为825.1,平均分约为75.01。那是不是这4个班的成绩就差不多了呢?
波动情况
邓老师正纳闷,旁边的唐老师见状,凑近一看说:“邓老师,你这个方法会有误差哦。”
“虽然各个班的平均分差不多,但很可能情况不一样:比如有的班成绩特别好和成绩特别差的都比较多,波动很大。有的班成绩都比较平均,差距不大。
这样两个班的情况就会非常不同了,教学策略也会不一样。”
“那我要怎么计算成绩的波动呢?”邓老师很好奇。
“其实你可以用标准差来计算成绩的波动幅度,标准差的值越高说明成绩波动越大。”唐老师建议到。
邓老师在唐老师的建议下,计算出了各个班的标准差,却吃惊地发现:
咦?各个班的文科成绩和理科成绩的标准差竟然也差不多。看来各个班的成绩波动也都是相似的。
邓老师还有一个猜测:会不会这几个班成绩差不多,但是偏科比较严重呢?比如有的班文科成绩特别好,理科成绩特别不好。
张老师路过,听到了他们的讨论,忍不住说:“试试计算一下相关系数呢,如果相关系数越高,说明文科成绩和理科成绩的关联度比较高,也就是文科成绩好,理科成绩也比较好,如果相关系数很低,那就可能是偏科很严重,文科成绩好但理科成绩很差。”
邓老师经过一通计算,又得出一个非常震惊的结果:
每个班级文科(语文+英语)和理科(数学+物理)的相关系数都是0.82。
不仅不偏科,水平几乎完全一样。
有了这几份统计学数据作支撑,邓老师立即决定下个月1,2,3,4班的都设定相同的教学提升计划。
教学总监看到这份计划,有些疑惑,建议邓老师将学生成绩画出图表来仔细分析。没想到,图表显示的结果。。。。。完全不相同!
1班的成绩比较分散,有波动。
2班成绩分布呈抛物线趋势。
3班成绩几乎都是线性分布,有一位同学的文科成绩非常高。
而4班的成绩更为神奇,10位同学的文科成绩几乎都相同,只有一位同学特别出类拔萃。
幸好通过图表发现了数据的异常,如果只是迷信数据分析的结果,给出的教学计划显然是不合理的。
安斯科姆四重奏
其实刚刚那组数据并不是邓老师统计的,而是统计学家弗朗西斯·安斯库姆(Francis Anscombe),在1973年构造的。
这位统计学家在和数据打了很多年交道后发现,仅仅依赖概括性统计度量,可能具有误导性,而挖掘数据的视觉模式,趋势和异常值反而更加重要。
于是构造了这组统计特性一致,绘制出的图表则截然不同的数据,让大家了解数据可视化的重要性。
彩蛋
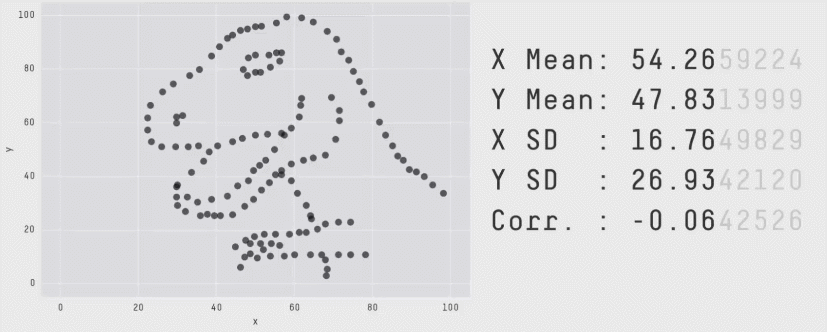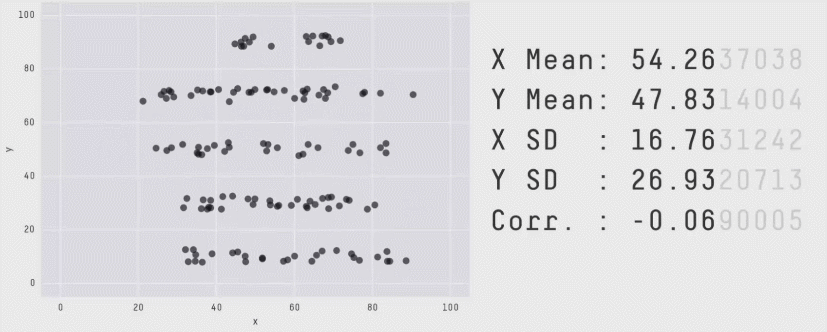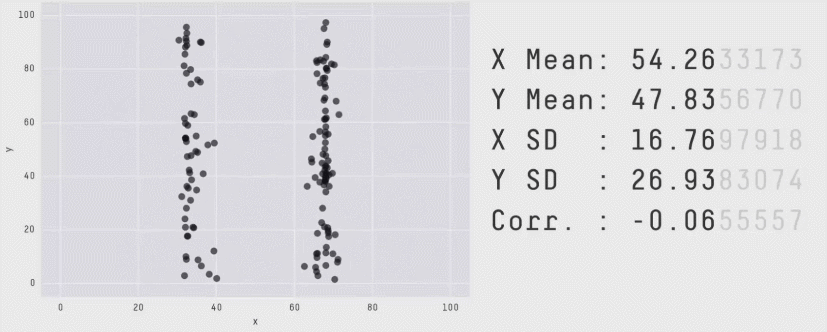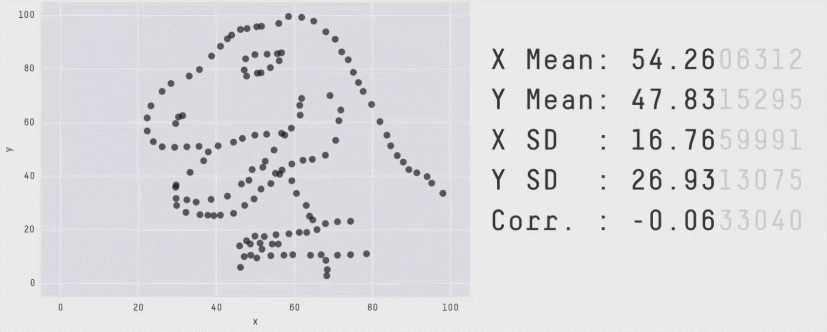
除此之外,美国迈阿密大学教授Alberto Cairo也曾构造了一组统计学意义上相同,画出来的图表完全不同的数据,如图所示,是不是很神奇呢?
选择图表
数据可视化如此重要,学会制作严谨而科学的图表就显得非常重要了。
今天咱们先迈出数据可视化的第一步:选择图表。
在不同的场景中,我们所得到的数据不同,想要获取的信息不同,所以选择的图表也不同。
根据数据关系图表可以分为:比较、趋势、构成、联系四种类型。
接下来我们将针对这四种类型的数据关系,来介绍每种关系下常见的图表类型。
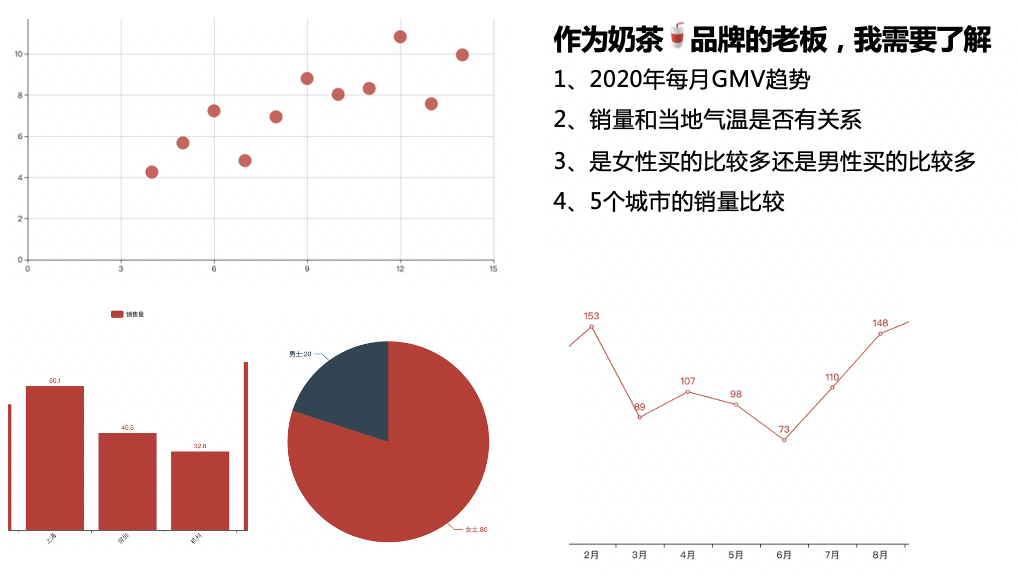
比较-柱状图
定义:柱状图,又称长条图、柱形图,是一种以长方形的长度为变量的统计图表。
应用:柱状图能够反应数据间的差异,一般用来进行分类项目间的比较。
注意:柱状图仅适用于中小规模数据集,超过10个就不建议使用哦。
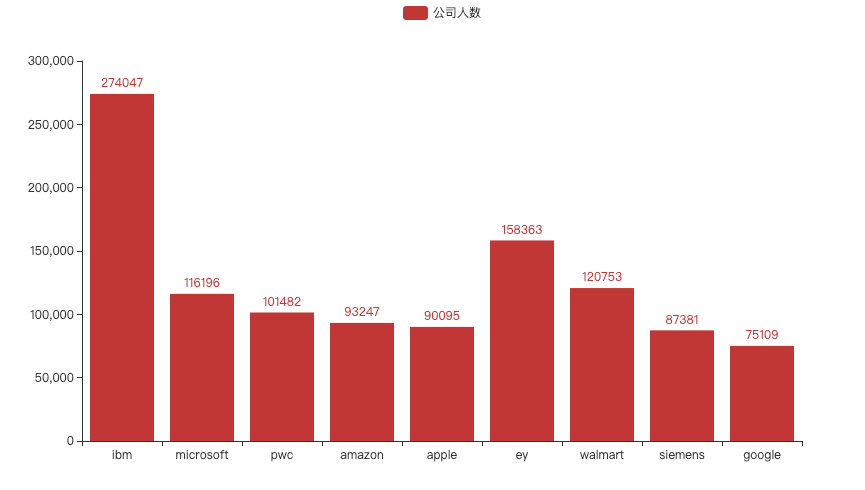
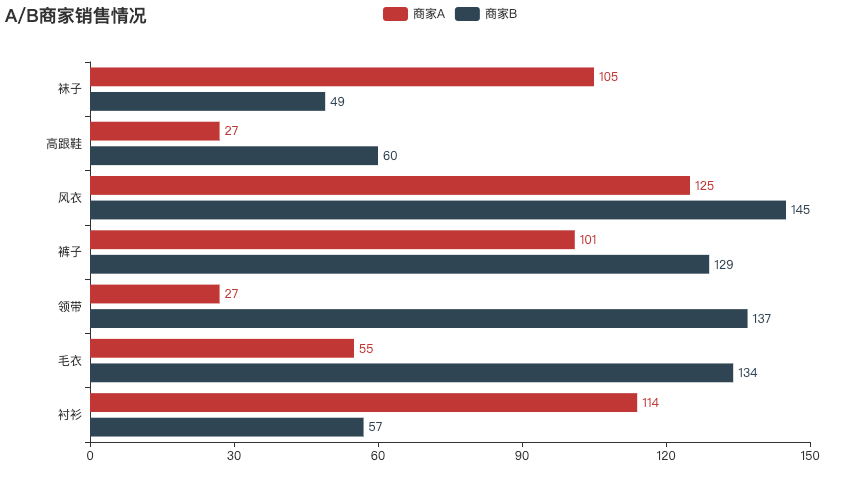
比较—条形图
定义:条形图(bar chart)简单来说就是横着排列的柱状图。
应用:条形图和柱状图都可以进行数据间的比较,不过当数据较多,比如超过10项时,需要使用条形图。
例如:2020年全球30个国家的GDP对比。
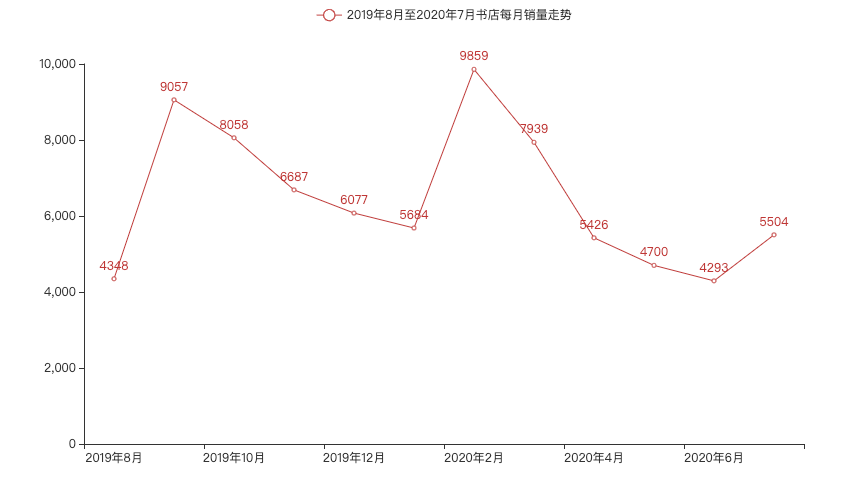
趋势-折线图
定义:以折线的上升或下降来表示统计数量的增减变化的统计图,叫作折线统计图。
应用:折线图可以显示随时间而变化的连续数据,非常适用于显示在相等时间间隔下数据的趋势。
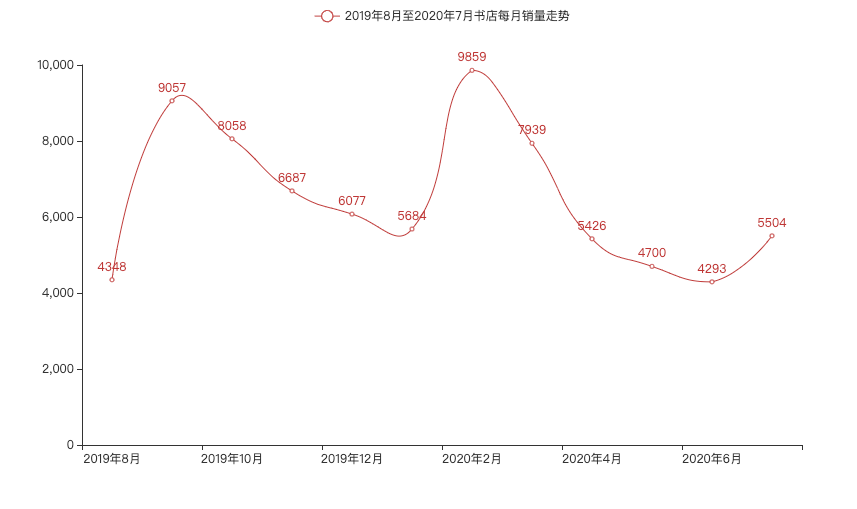
趋势—平滑折线图
- 定义:平滑折线图是显示随时间而变化的连续数据,主要用于反应数据的整体趋势。
- 应用:如果时间跨度大或者数据波动比较大时,可以使用平滑折线图,因为此时使用折线图显得较乱,光滑折线图则比较清晰。
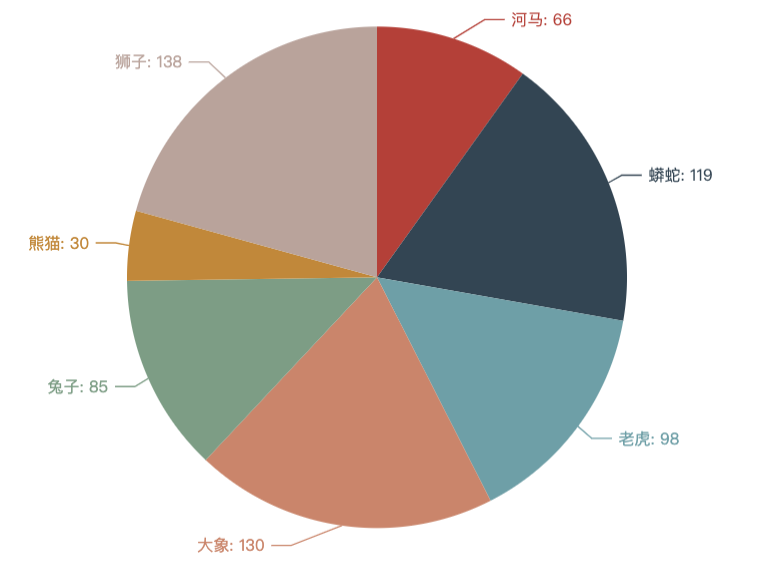
构成—饼图
定义:饼图,是一个划分为几个扇形的圆形统计图表,用于描述量、频率或百分比之间的相对关系。
应用:在需要描述某一部分占总体的百分比时,适合使用饼图。
例如:占据公司全部资金一半的两个渠道;某公司员工的男女比例等。
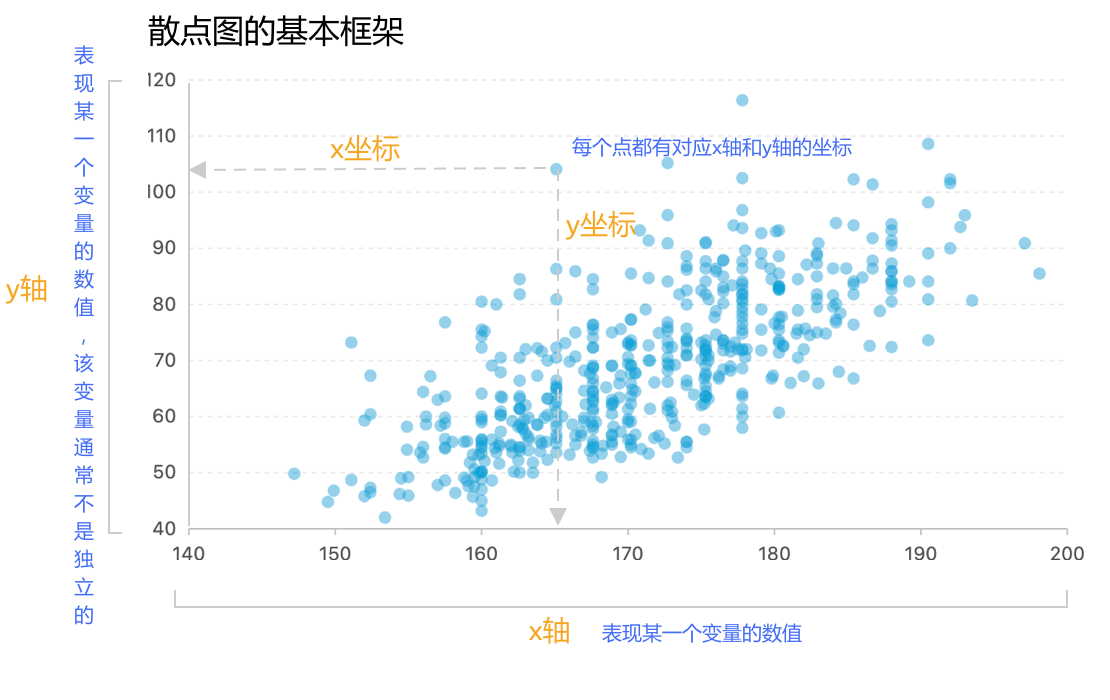
散点图
定义: 散点图也叫 X-Y图,它将所有的数据以点的形式展现在直角坐标系上,以显示变量之间的相互影响程度,点的位置由变量的数值决定。
应用:分析坐标点的分布情况,判断两个变量(数据)之间的关联或分布趋势。
例如:体重和身高的关系,GDP与房价的关系。
联系—气泡图
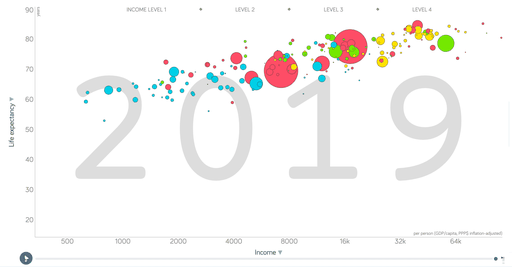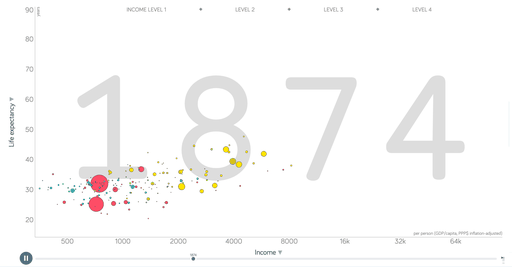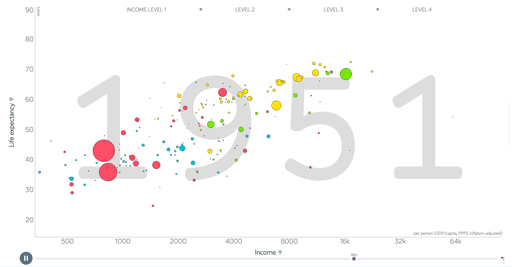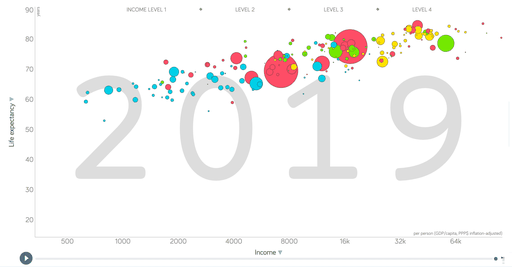
- 定义:气泡图通常是用来表述三个数据之间的关系,或者同时呈现三维数据。简单来说就是在散点图的基础上加上散点大小这个维度来进行比较。
- 应用:例如统计学家汉斯.罗林在Ted演讲中用到的这个图,展示了200个国家:人均收入、寿命、人口。气泡基本分布在一条斜线上,人均收入和寿命有一定相关性。
应用场景总结
分类比较:柱状图
变化趋势:折线图
总体构成:饼图
相关关系:散点图
更多的图表类型
除此之外,还有很多不同的图表类型,比如:
地理位置:地图
流量分布:桑基图
关系:关系图
部分与整体:漏斗图我们会在后面的课程中继续学习。
Why pyecharts
在Python中可以用于制作图表的模块非常多,我们选择使用pyecharts,因为 :
API设计简洁,使用简单
有30+常见的交互式图表,配置灵活,图表精美
多达400+地图文件以及原生的百度地图,为地理数据可视化提供强有力的支持
模块更新频率高,使我们可以用上最新的特性和图表