回溯算法

关于回溯算法的介绍：回溯其实就存在于递归函数下面，回溯算法是一种暴力搜索法。对于一些问题来说，能够使用暴力搜索法解决就已经很好了，使用一层一层的for循环嵌套，根本都搜索不出来的时候，使用回溯算法就可以搜索出所有解法。

回溯算法能够解决的问题：

1. 组合问题

   如：给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

   candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

2. 切割问题

   如：给你一个字符串，问如何切割才能保证所有子字符串都是回文字符串，问有几种切割方式

3. 子集问题

   如：求数组{1,2,3,4}的所有子集

4. 排列问题

5. 棋盘问题：N皇后、解数独

回溯算法的模板：

// 回溯递归函数一般没有返回值，参数值比较多
void backTracking(paramter paramters){
  // 设置终止条件，因题目设定而异
	if (终止条件满足){
	  收集结果;
	  return;
	}
	
	// 单层搜索，对每一个元素做处理
	for (int i=0; i < n; i++){
	  // 对每个元素做处理
	  path.append(i);
	  backTracking(路径，选择列表); // 递归
	  path.removeLast(i); // 回溯
	}
}

组合问题

1. 问题描述：

   给你一个无重复元素的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的所有不同组合 ，并以列表形式返回。你可以按任意顺序返回这些组合。candidates 中的同一个数字可以无限制重复被选取。如果至少一个数字的被选数量不同，则两种组合是不同的。

   示例：

   输入：candidates = [2,3,6,7], target = 7
   输出：[[2,2,3],[7]]

   思路：

   首先，由于不知道给定的整数数组的长度，显然用for循环解决不了这个问题。这时候，就需要用到回溯算法来暴力搜索所有的解法。使用回溯算法，最好要画出它的树形图，此题如下：

   

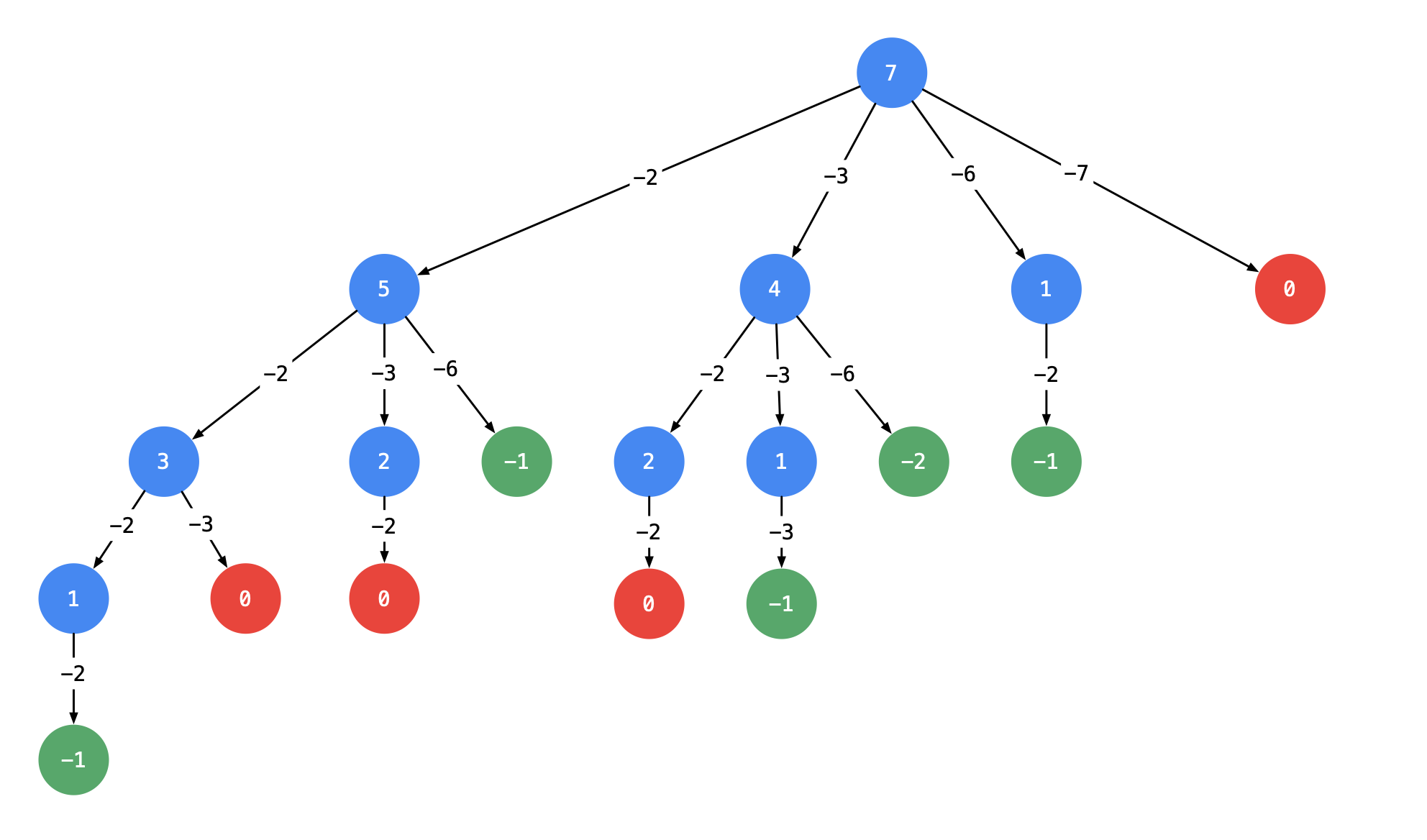
   说明：

   • 以 target = 7 为 根结点 ，创建一个分支的时候做减法 ；
   • 每一个箭头表示：从父亲结点的数值减去边上的数值，得到孩子结点的数值。边的值就是题目中给出的 candidate 数组的每个元素的值；
   • 减到 0 或者负数的时候停止，即：结点 0 和负数结点成为叶子结点；
   • 所有从根结点到结点 0 的路径（只能从上往下，没有回路）就是题目要找的一个结果。

   为了避免重复，很显然，前一个分支使用过的元素，后一个分支不能再使用了，如图：

   

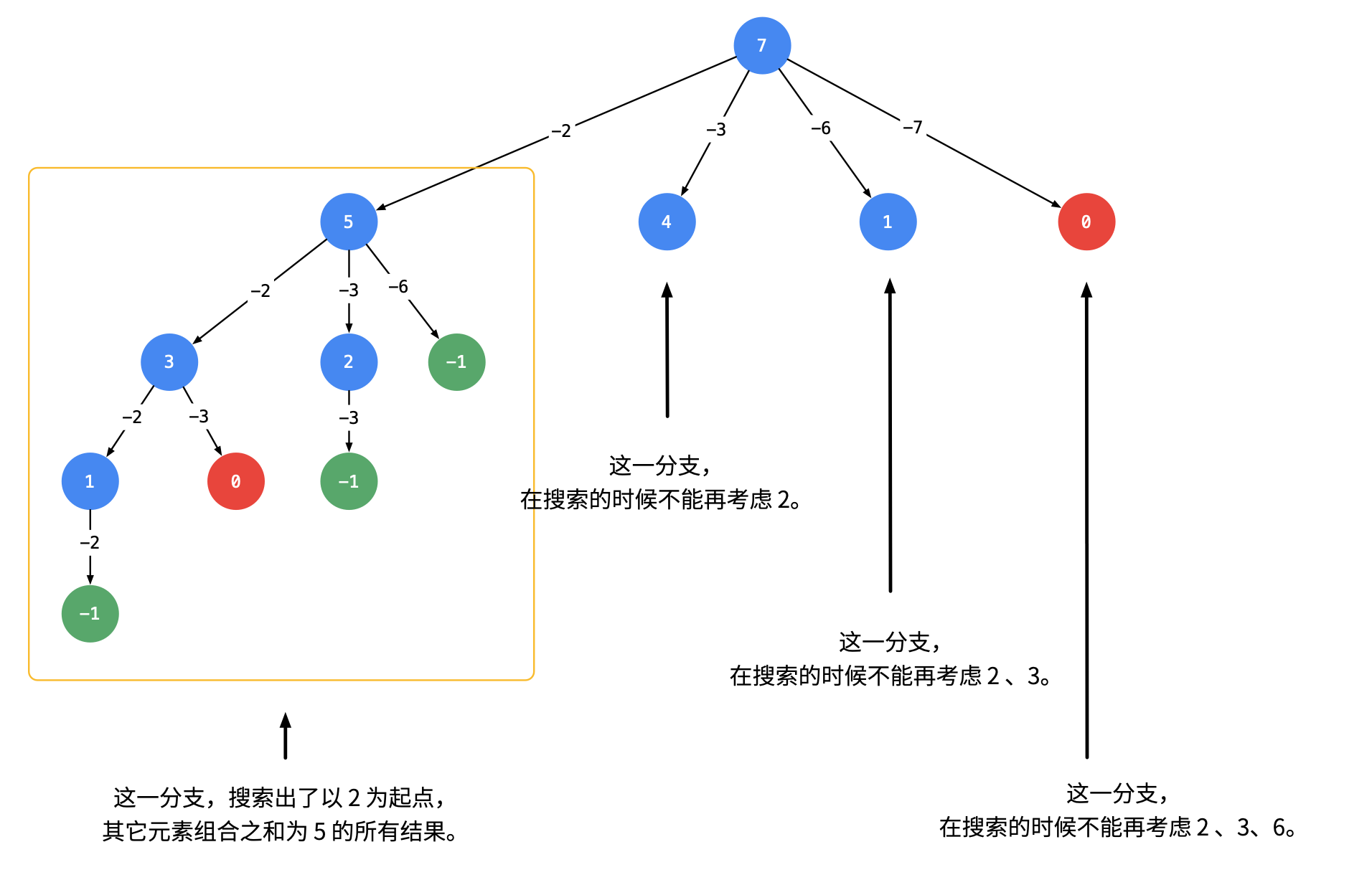
   代码如下（进行了一些剪枝操作）：

   class Solution {

       public List<List<Integer>> combinationSum(int[] candidates, int target) {
           List<Integer> path = new ArrayList<>();
           List<List<Integer>> solutionSets = new ArrayList<>();
           Arrays.sort(candidates);
           backtracking(candidates, target, 0, path, solutionSets);
           return solutionSets;
       }
   
       public void backtracking(int[] candidates, int target, int startIndex, List<Integer> path, List<List<Integer>> solutionSets){
           // 回溯算法终止条件
           if (target<0){
               return;
           }
           if (target==0){
               // 收集结果
               solutionSets.add(new ArrayList<>(path));
           } 
   
           // 单层搜索
           for (int i=startIndex; i < candidates.length; i ++){
               // 剪枝操作
               if(candidates[i] > target){
                   return;
               }
               // 对元素进行处理
               path.add(candidates[i]);
               backtracking(candidates, target-candidates[i], i, path, solutionSets); // 递归
               path.remove(path.size()-1); // 回溯
           }
       }
   }